线性回归

当我们学习一门新课程、接触一个新专业时，总会对该领域的专有名词感到困惑，甚至看完解释仍难以理解其含义。在此，我告诉大家一个我自悟的一个学习方法，就是弄明白这个专有名词的起源，知道它产生的源头，也就是说它产生的历史场景和上下文，比如我们都听说过：君子固穷，平贱夫妻百事哀等等成语和诗句，如果单从字面意思去理解都是有失偏颇的，当你去找到这些成语和诗句的出处，你就会恍然大悟。

譬如今天要学的线性“回归”，这个回归（regression）和我们平时说的“回归故里”的回归（return）是两个含义完全不同的词，如果想弄明白这个词的含义，我们需要去追根溯源，我们发现线性方程：y=ax + b 就叫做回归。这个时候我们应该去思考这个方程是怎么产生的，任何理论和公式的产生都离不开应用需求，人们经常想找到一种简洁方面的方法去套用在繁琐的事情上，比如在古代买卖土地，人们发现土地的面积和价钱之间的有一定的关系，如果能找到一种公式去描述这种关系，我们就可以根据土地的面积预测出能卖多少钱。我们可以根据大量的样本（各种土地买卖的数据）来总结一种普遍适用的公式。这种根据样本结果去推导出一种普遍适用公式的方法就叫做“回归”。

一元线性回归

线性回归可以说是用法非常简单、用处非常广泛、含义也非常容易理解的一类算法，作为机器学习的入门算法非常合适。我们上中学的时候，都学过二元一次方程，我们将y作为因变量，x 作为自变量，得到方程：$y={\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}_0+{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}_{1}x$，当给定参数和的时候，画在坐标图内是 一条直线（这就是“线性”的含义）。

当我们只用一个 x 来预测 y，就是一元线性回归，也就是在找一个直线来拟合数据。比如，我有一组数据画出来的散点图，横坐标代表广告投入金额，纵坐标代表销售量，线性回归就是要找一条直线，并且让这条直线尽可能地拟合图中的数据点。

这里我们得到的拟合方程是 $y=0.0512x+7.1884$，此时当我们获得一个新的广告投入金额后，我们就可以用这个方程预测出大概的销售量。

数学理论的世界是精确的，譬如你代入 $x=0$ 就能得到唯一的$\stackrel{\wedge \; <!--\; logical\; and\; -->}{y}$，$\stackrel{\wedge \; <!--\; logical\; and\; -->}{y}$=7.1884（y 上面加一个小帽子 hat，表示这个不是我们真实观测到的，而是估计值）。但现实世界中的数据就像这个散点图，我们只能尽可能地在杂乱中寻找规律。用数学的模型去拟合现实的数据，这就是统计。统计不像数学那么精确，统计的世界不是非黑即白的，它有“灰色地带”，但是统计会将理论与实际间的差别表示出来，也就是“误差”。

损失函数

那既然是用直线拟合散点，为什么最终得到的直线是$y=0.0512x+7.1884$，而不是下图中的$y=0.0624x+5$呢？这两条线看起来都可以拟合这些数据啊？毕竟数据不是真的落在一条直线上，而是分布在直线周围，所以我们要找到一个评判标准，用于评价哪条直线才是最“合适”的。

我们先从残差说起。残差说白了就是真实值和预测值间的差值（也可以理解为差距、距离），用公式表示是：$e=y-{\stackrel{\wedge \; <!--\; logical\; and\; -->}{y}}^{}$

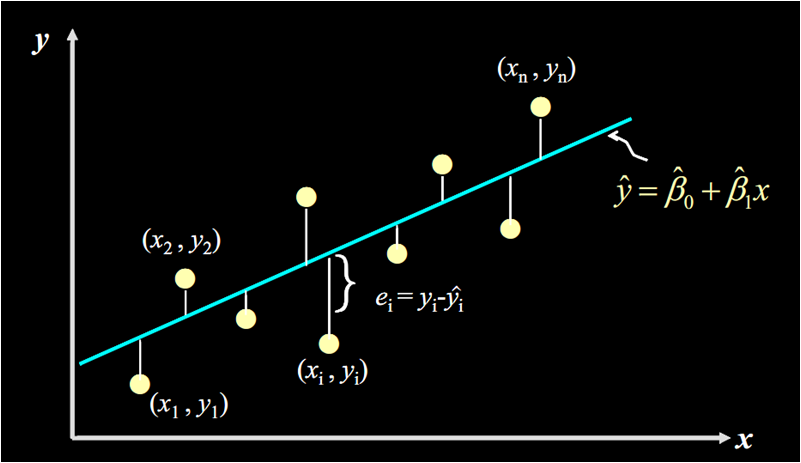
我们举例子：假定对于某个广告投入$x_i$，我们有对应的实际销售量$y_i$，和预测出来的销售量 ${\stackrel{\wedge \; <!--\; logical\; and\; -->}{y}}_i$（通过将代入公式$y={\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}_0+{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}_{1}x$计算得到），计算$e_i=y_i-{\stackrel{\wedge \; <!--\; logical\; and\; -->}{y}}_i$的值，再将其平方（为了消除负号），对于我们数据中的每个点如此计算一遍，再将所有的$e_i^2$相加，就能量化出拟合的直线和实际之间的误差。

用公式表示就是：$Q=\underset{1}{\overset{n}{\sum \; <!--\; n-ary\; summation\; -->}}{(y_i-{\stackrel{\wedge \; <!--\; logical\; and\; -->}{y}}_i)}^2=\underset{1}{\overset{n}{\sum \; <!--\; n-ary\; summation\; -->}}(y_i-{({\stackrel{\wedge \; <!--\; logical\; and\; -->}{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}}_0+{\stackrel{\wedge \; <!--\; logical\; and\; -->}{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}}_1{x}_i)}^2$

这个公式是残差平方和，即SSE（Sum of Squares for Error），在机器学习中它是回归问题中最常用的损失函数。

现在我们知道了损失函数是衡量回归模型误差的函数，也就是我们要的“直线”的评价标准。这个函数的值越小，说明直线越能拟合我们的数据。如果还是觉得难理解，我下面就举个具体的例子。

用文章开头的例子，假设我们有一组样本，建立了一个线性回归模型$f\left(x\right)$，其中一个样本A是这样的：公司投入了$x=1000$元做广告，销售量为 $y=60$，$f(x=1000)$算出来是 50，有 -10 的偏差。

样本 B：$x=2000$，销售量为 $y=95$，$f(x=2000)=10$，偏差为 5。

样本 C： $x=3000$，销售量为 $y=150$，$f(x=2000)=150$，偏差为 0 哦，也就是没有偏差~

要计算 A、B、C 的整体偏差，因为有正有负，所以做个平方，都弄成正的，然后再相加，得到总偏差，也就是平方损失，是 125。

最小二乘法

我们不禁会问，这个和的具体值究竟是怎么算出来的呢？

我们知道，两点确定一线，有两组 $x$，$y$ 的值，就能算出来和。但是现在我们有很多点，且并不正好落在一条直线上，这么多点每两点都能确定一条直线，这到底要怎么确定选哪条直线呢？

当给出两条确定的线，如 $y=0.0512x+7.1884$，$y=0.0624x+5$ 时，我们知道怎么评价这两个中哪一个更好，即用损失函数评价。那么我们试试倒推一下？

以下是我们的数据公式推导，我尽量对每个公式作解释说明。

给定一组样本观测值：（$i=1,2,3\dots \; <!--\; horizontal\; ellipsis\; -->n$ ），要求回归函数尽可能拟合这组值。普通最小二乘法给出的判断标准是：残差平方和的值达到最小。我们再来看一下残差平方和的公式：$Q=\underset{1}{\overset{n}{\sum \; <!--\; n-ary\; summation\; -->}}{(y_i-{\stackrel{\wedge \; <!--\; logical\; and\; -->}{y}}_i)}^2=\underset{1}{\overset{n}{\sum \; <!--\; n-ary\; summation\; -->}}(y_i-{({\stackrel{\wedge \; <!--\; logical\; and\; -->}{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}}_0+{\stackrel{\wedge \; <!--\; logical\; and\; -->}{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}}_1{x}_i)}^2$

这个公式是一个二次方程，我们知道一元二次方程差不多长下图这样：

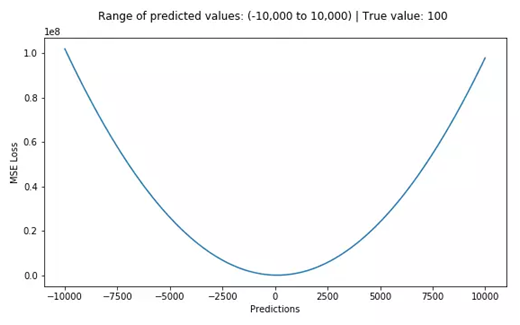
上面公式中 ${\stackrel{\wedge \; <!--\; logical\; and\; -->}{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}}_0$ 和 ${\stackrel{\wedge \; <!--\; logical\; and\; -->}{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}}_1$ 未知，有两个未知参数的二次方程，画出来是一个三维空间中的图像，类似下面：

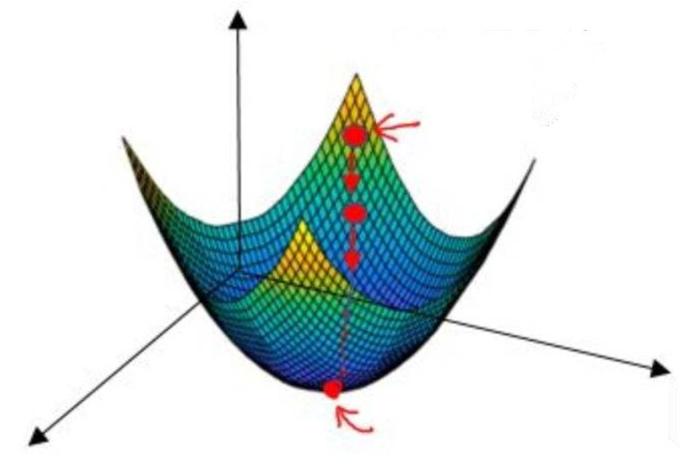
这类函数在数学中叫做凸函数，关于什么凸函数的数学定义，还记得微积分知识的话，就知道导数为 0 时，Q 取最小值，因此我们分别对 $\stackrel{\wedge \; <!--\; logical\; and\; -->}{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}$ 和 ${\stackrel{\wedge \; <!--\; logical\; and\; -->}{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}}_1$ 求偏导并令其为 0：

$\frac{\partial \; <!--\; partial\; differential\; -->Q}{\partial \; <!--\; partial\; differential\; -->{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}_0}=2\underset{1}{\overset{n}{\sum \; <!--\; n-ary\; summation\; -->}}(y_i-{\stackrel{\wedge \; <!--\; logical\; and\; -->}{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}}_0-{\stackrel{\wedge \; <!--\; logical\; and\; -->}{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}}_1{x}_i)=0$

$\frac{\partial \; <!--\; partial\; differential\; -->Q}{\partial \; <!--\; partial\; differential\; -->{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}_1}=2\underset{1}{\overset{n}{\sum \; <!--\; n-ary\; summation\; -->}}(y_i-{\stackrel{\wedge \; <!--\; logical\; and\; -->}{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}}_0-{\stackrel{\wedge \; <!--\; logical\; and\; -->}{\mathrm{\beta \; <!--\; greek\; small\; letter\; beta\; -->}}}_1{x}_i)x_i=0$

$x_i$，$y_i$（i=$i=1,2,3\dots \; <!--\; horizontal\; ellipsis\; -->n$ 都是已知的，全部代入上面两个式子，就可求得和的值啦。这就是最小二乘法，“二乘”是平方的意思。

多元线性回归

线性回归的定义，是利用最小二乘函数对一个或多个自变量之间关系进行建模的方法。现在我们看这个定义，是不是觉得不难理解了呢？

以上举的例子是一维的例子（$x$ 只有一个），如果有两个特征，就是二元线性回归，要拟合的就是二维空间中的一个平面。如果有多个特征，那就是多元线性回归。

最后再提醒一点，做线性回归，不要忘了前提假设是y和x呈线性关系，如果两者不是线性关系，就要选用其他的模型啦。

自行实现线性回归

说明：下面代码大家不需要自己写出来，以后我们也不用自己写代码实现线性回归。我们自行写代码实现线下回归是为了让大家留个印象。

我们已经了解了线性回归的前世今生，现在就让我们写代码来实现线性回归吧。

首先我们自动生成一些数据集，我们人为制造一些符合类似一元一次方程的数据（$x$ 和 $y$），然后添加一些噪音（更符合现实情况），然后我们开始写代码看看能否得到类似的一元一次方程。

def Linear_regression():
    k = 3.0  # 初始化k的值
    b = 2.0  # 初始化b的值
    NUM_SAMPLES = 100  # 100 个样本
    x = np.random.normal(size=[NUM_SAMPLES, 1])  # 随机生成样本X数据集
    noise = np.random.normal(size=[NUM_SAMPLES, 1])  # 随机生成噪音

    # 定义 y = kx + b, noise 为添加的噪声
    y = k * x + b + noise

方程我们定义好了，然后，我们开始写个优化器，定义学习率，然后使用梯度下降的方式降低误差，是我们的方程更符合数据集的线性回归。

def optimizer(X, Y, starting_b, starting_m, NUM_SAMPLES):
    b = starting_b
    k = starting_m
    learning_rate = 0.1  # 学习率
    for i in range(NUM_SAMPLES):
        b, k = compute_gradient(b, k, X, Y, learning_rate)
        if i % 100 == 0:
            print('iter {0}:error={1}'.format(i, compute_error(b, k, X, Y)))
    return [b, k]

其中 compute_gradient 是我们自己实现的梯度下降算法。该算法的目的就是不停的调整k和b的值，使其根据数据集得到更准确的线性回归。

def compute_gradient(b_current, m_current, x, y, learning_rate):
    N = float(len(x))
    b_gradient = -(2 / N) * (y - m_current * x - b_current)
    b_gradient = np.sum(b_gradient, axis=0)  # 正在调整的b的值

    m_gradient = -(2 / N) * x * (y - m_current * x - b_current)
    m_gradient = np.sum(m_gradient, axis=0)  # 正在调整的m的值

    new_b = b_current - (learning_rate * b_gradient)
    new_m = m_current - (learning_rate * m_gradient)
    return [new_b, new_m]

梯度下降算法，就是根据学习率，不停的调整k和b值让损失值更小。我们在代码中每次训练一次后，都打印出损失值，我们发现这个损失值越来越小。

def optimizer(x, y, starting_b, starting_m, NUM_SAMPLES):
    b = starting_b
    k = starting_m
    learning_rate = 0.1  # 学习率
    for i in range(NUM_SAMPLES):
        b, k = compute_gradient(b, k, x, y, learning_rate)
        if i % 100 == 0:
            print('iter {0}:error={1}'.format(i, compute_error(b, k, x, y)))
    return [b, k]

其中 compute_error 函数是我们自己定义的损失函数。

def compute_error(b, k, x, y):
    totalError = (y - k * x - b) ** 2
    totalError = np.sum(totalError)
    return totalError / float(len(x))  # 均方误差

最后，我们训练 1000 次，得到 k 和 b 的值，有了这两个值就可以画出线性回归的结果。

# 通过1000次迭代求出b和k的值
[b, k] = optimizer(x, y, b, k, 1000)

# 画出线性回归的结果
y_predict = k * x + b
pylab.plot(x, y, 'o')
pylab.plot(x, y_predict, 'k-')
pylab.show()

得到的线性回归的图形如下：当然，我们可以通过增加训练次数，让线性回归更精确。

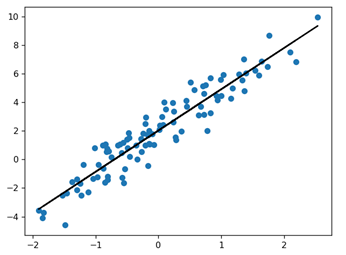
我们整理一下整个线性回归的完整代码如下：

import numpy as np
import pylab

'''
每次向下滑要慢慢滑，就是要个步长，我们定义为 learning_rate,往往很小的一个值。
向下滑动的次数，就是迭代的次数，我定义为 1000,相对 learning_rate 往往很大。
定义好这两个，我们就可以一边求梯度，一边向下滑了。就是去更新 k 和 b。
'''

def compute_error(b, k, x, y):
    totalError = (y - k * x - b) ** 2
    totalError = np.sum(totalError)
    return totalError / float(len(x))  # 均方误差


def optimizer(x, y, starting_b, starting_m, NUM_SAMPLES):
    b = starting_b
    k = starting_m
    learning_rate = 0.1  # 学习率
    for i in range(NUM_SAMPLES):
        b, k = compute_gradient(b, k, x, y, learning_rate)
        if i % 100 == 0:
            print('iter {0}:error={1}'.format(i, compute_error(b, k, x, y)))
    return [b, k]


def compute_gradient(b_current, m_current, x, y, learning_rate):
    N = float(len(x))
    b_gradient = -(2 / N) * (y - m_current * x - b_current)
    b_gradient = np.sum(b_gradient, axis=0)  # 正在调整的b的值

    m_gradient = -(2 / N) * x * (y - m_current * x - b_current)
    m_gradient = np.sum(m_gradient, axis=0)  # 正在调整的m的值

    new_b = b_current - (learning_rate * b_gradient)
    new_m = m_current - (learning_rate * m_gradient)
    return [new_b, new_m]


def Linear_regression():
    k = 3.0  # 初始化k的值
    b = 2.0  # 初始化b的值
    NUM_SAMPLES = 100  # 100 个样本
    x = np.random.normal(size=[NUM_SAMPLES, 1])  # 随机生成样本X数据集
    noise = np.random.normal(size=[NUM_SAMPLES, 1])  # 随机生成噪音

    # 定义  y = kx + b, noise 为添加的噪声
    y = x * k + b + noise

    # 通过1000次迭代求出b和k的值
    [b, k] = optimizer(x, y, b, k, 1000)

    # 画出线性回归的结果
    y_predict = k * x + b
    pylab.plot(x, y, 'o')
    pylab.plot(x, y_predict, 'k-')
    pylab.show()

# 调用线性回归
Linear_regression()

Tensorflow 实现线性回归

说明：我们先了解 Tensorflow 里面含有大量的函数可以让我们更简单的实现线性回归。下面代码中的一些函数解析，等我们学完神经网络自然就明白了，现在先留个印象即可。。

线性回归是机器学习中最简单的问题，同时线性回归也与人工神经网络有千丝万缕的关系。前面我们已经了解线性回归的来龙去脉，在此我们将以线性回归为例，使用 TensorFlow 2.x 提供的 API 来进行实现。

线性回归是入门机器学习必学的算法，其也是最基础的算法之一。接下来，我们以线性回归为例，使用 TensorFlow 2.0 提供的 API 和 Eager Execution 机制对其进行实现。

TensorFlow 2.x 有两种 API 可以实现线性回归，我们把原生的 API 叫低阶 API，对新增加 keras 提供的 API 叫高阶 API，在此我们会把这两种方式一一实现。

低阶 API 实现，实际上就是利用 Eager Execution 机制来完成。实验首先初始化一组随机数据样本，并添加噪声，然后将其可视化出来。代码和对应的样本集如下图。

import matplotlib.pyplot as plt
import tensorflow as tf
from pylab import mpl

mpl.rcParams['font.sans-serif'] = ['Microsoft YaHei']  # 指定默认字体：解决plot不能显示中文问题
mpl.rcParams['axes.unicode_minus'] = False             # 解决保存图像是负号'-'显示为方块的问题

# 初始化k和b，并生成100个样本
K = 3.0
B = 2.0
NUM_SAMPLES = 100

# 样本（特征值，标签）
X = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()  # 初始化随机样本数据X

noise = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()  # noise为人为添加的噪声
Y = K * X + B + noise  # 根据 X 生成随机样本数据 Y

# 画出样本 X 和标签 Y 在坐标上的散点图
plt.scatter(X, Y, label=u'X，Y 的坐标', color='g', s=10)
plt.xlabel(u'x轴')
plt.ylabel(u'y轴')
plt.legend()
plt.show()

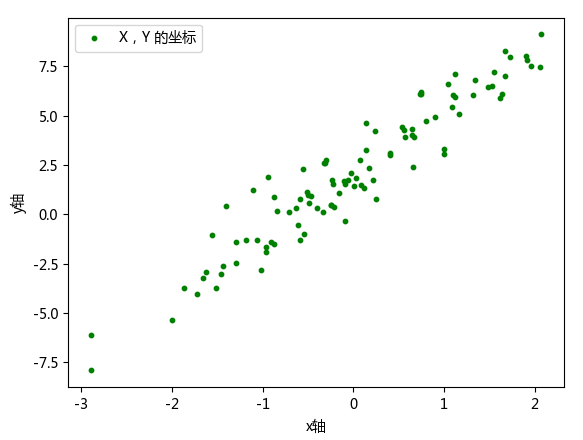
接下来，我们定义一元线性回归模型：

$f(w,b,x)=wx+b$

这里我们构建自定义模型类，并使用 TensorFlow 提供的 tf.Variable 随机初始化参数 w 和截距项 b。

class Model(object):
    def __init__(self):
        self.W = tf.Variable(tf.random.uniform([1]))  # 随机初始化参数
        self.b = tf.Variable(tf.random.uniform([1]))

    def __call__(self, x):
        return self.W * x + self.b  # w * x + b

对于随机初始化的 w 和 b，我们可以将其拟合直线绘制到样本散点图中。

import tensorflow as tf
import matplotlib.pyplot as plt
from pylab import mpl

mpl.rcParams['font.sans-serif'] = ['Microsoft YaHei']  # 指定默认字体：解决plot不能显示中文问题
mpl.rcParams['axes.unicode_minus'] = False             # 解决保存图像是负号'-'显示为方块的问题

# 初始化k和b，并生成100个样本
K = 3.0
B = 2.0
NUM_SAMPLES = 100

X = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()      # 初始化随机样本数据X
noise = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()  # noise为人为添加的噪声
Y = K * X + B + noise  # 根据X生成随机样本数据Y

class Model(object):
    def __init__(self):
        self.W = tf.Variable(tf.random.uniform([1]))  # 随机初始化参数
        self.b = tf.Variable(tf.random.uniform([1]))

    def __call__(self, x):
        return self.W * x + self.b  # w*x + b


model = Model()  # 实例化模型

# 画出样本 X 和标签 Y 在坐标上的散点图以及随机拟合的一条直线
plt.plot(X, model(X), label=u'随机拟合的直线', c='r')  # 随机拟合的一条直线
plt.scatter(X, Y, label=u'X，Y 的坐标', color='g', s=10)  # X，Y 的散点坐标
plt.xlabel(u'x轴')
plt.ylabel(u'y轴')
plt.legend()
plt.show()

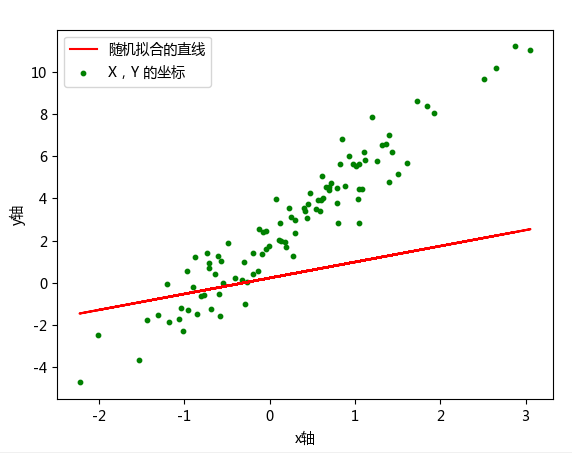
可以明显看出，直线并没有很好地拟合样本。当然，由于是随机初始化，也有极小概率一开始拟合效果非常好，那么重新执行一次上面的单元格另外随机初始化一组数据即可。

然后，我们定义线性回归使用到的损失函数。这里使用线性回归问题中常用的平方损失函数。对于线性回归问题中与数学相关的知识点，我们刚刚讲解过：

$Loss(w,b,x,y)=\underset{i=1}{\overset{n}{\sum \; <!--\; n-ary\; summation\; -->}}{(f(w,b,x_i)-y_i)}^2$

Tensorflow 提供的 reduce_mean 函数实现了上述公式，根据公式实现损失计算函数。

def loss_fn(model, x, y):
    y_ = model(x)
    return tf.reduce_mean(tf.square(y_ - y))

接下来，就可以开始迭代过程了，这也是最关键的一步。使用迭代方法求解线性回归的问题中，我们首先需要计算参数的梯度，然后使用梯度下降法来更新参数。

$w\leftarrow \; <!--\; leftwards\; arrow\; -->w-1r*\frac{\partial \; <!--\; partial\; differential\; -->loss(w,b)}{\partial \; <!--\; partial\; differential\; -->w}$

$b\leftarrow \; <!--\; leftwards\; arrow\; -->b-\mathrm{l}r*\frac{\partial \; <!--\; partial\; differential\; -->loss(w,b)}{\partial \; <!--\; partial\; differential\; -->b}$

上面公式中，lr 指学习率。

TensorFlow 2.0 中的 Eager Execution 提供了 tf.GradientTape 用于追踪梯度。所以，下面我们就实现梯度下降法的迭代更新过程。

EPOCHS = 100
LEARNING_RATE = 0.1
for epoch in range(EPOCHS):  # 迭代次数
    with tf.GradientTape() as tape:  # 追踪梯度
        loss = loss_fn(model, X, Y)  # 计算损失
    dW, db = tape.gradient(loss, [model.W, model.b])  # 计算梯度
    model.W.assign_sub(LEARNING_RATE * dW)  # 更新梯度
    model.b.assign_sub(LEARNING_RATE * db)
    # 输出计算过程
    print('Epoch [{}/{}], loss [{:.3f}], W/b [{:.3f}/{:.3f}]'.format(epoch, EPOCHS, loss,
                                                                     float(model.W.numpy()),
                                                                     float(model.b.numpy())))

上面的代码中，我们初始化 tf.GradientTape() 以追踪梯度，然后使用 tape.gradient 方法就可以计算梯度了。值得注意的是，tape.gradient() 第二个参数支持以列表形式传入多个参数同时计算梯度。紧接着，使用 .assign_sub 即可完成公式中的减法操作用以更新梯度。

下图显示随着训练次数的增加，损失值越来越小，w 和 b 也在更新。

最终，我们绘制参数学习完成之后，模型的拟合结果。

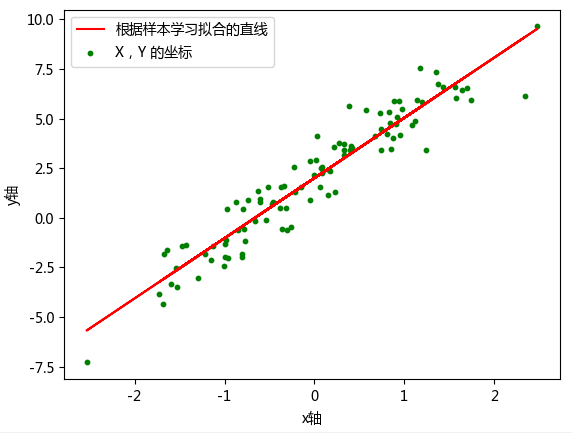
由于是随机初始化参数，如果迭代后拟合效果仍然不好，一般是迭代次数太少的原因。你可以重复执行上面的迭代单元格多次，增加参数更新迭代次数，即可改善拟合效果。此提示对后面的内容同样有效。

我们整理一下用 Tensorflow 实现线性回归的完整代码，如下：

import tensorflow as tf
import matplotlib.pyplot as plt
from pylab import mpl

mpl.rcParams['font.sans-serif'] = ['Microsoft YaHei']  # 指定默认字体：解决plot不能显示中文问题
mpl.rcParams['axes.unicode_minus'] = False             # 解决保存图像是负号'-'显示为方块的问题

# 初始化k和b，并生成100个样本
K = 3.0
B = 2.0
NUM_SAMPLES = 100

X = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()      # 初始化随机样本数据X
noise = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()  # noise为人为添加的噪声
Y = K * X + B + noise  # 根据X生成随机样本数据Y

class Model(object):
    def __init__(self):
        self.W = tf.Variable(tf.random.uniform([1]))  # 随机初始化参数
        self.b = tf.Variable(tf.random.uniform([1]))

    def __call__(self, x):
        return self.W * x + self.b  # w*x + b


def loss_fn(model, x, y):
    y_ = model(x)
    return tf.reduce_mean(tf.square(y_ - y))


model = Model()  # 实例化模型
EPOCHS = 100
LEARNING_RATE = 0.1
for epoch in range(EPOCHS):  # 迭代次数
    with tf.GradientTape() as tape:  # 追踪梯度
        loss = loss_fn(model, X, Y)  # 计算损失
    dW, db = tape.gradient(loss, [model.W, model.b])  # 计算梯度
    model.W.assign_sub(LEARNING_RATE * dW)  # 更新梯度
    model.b.assign_sub(LEARNING_RATE * db)
    # 输出计算过程
    print('Epoch [{}/{}], loss [{:.3f}], W/b [{:.3f}/{:.3f}]'.format(epoch, EPOCHS, loss,
                                                                     float(model.W.numpy()),
                                                                     float(model.b.numpy())))

# 画出样本 X 和标签 Y 在坐标上的散点图以及根据样本学习拟合的一条直线
plt.plot(X, model(X), label=u'根据样本学习拟合的直线', c='r')  # 根据样本学习拟合的一条直线
plt.scatter(X, Y, label=u'X，Y 的坐标', color='g', s=10)  # X，Y 的散点坐标
plt.xlabel(u'x轴')
plt.ylabel(u'y轴')
plt.legend()
plt.show()

TensorFlow 2.0 中还提供了大量的高阶 API 帮助我们快速构建所需模型，接下来，我们使用一些新的 API 来完成线性回归模型的构建。这里还是沿用上面提供的示例数据。

tf.keras 模块下提供的 tf.keras.layers.Dense 全连接层（线性层）实际上就是一个线性计算过程。所以，模型的定义部分我们就可以直接实例化一个全连接层即可。

上面我们使用的 TensorFlow API 实现过程实际上还不够精简，我们可以完全使用高阶 API 即 TensorFlow Keras API 来实现线性回归。

我们这里使用 Keras 提供的 Sequential 序贯模型结构。和上面的例子相似，向其中添加一个线性层。Keras 序贯模型第一层为线性层时，规定需指定输入维度，这里为 input_dim=1。

# 使用 tf 高阶 API keras
model = tf.keras.Sequential()
# 全连接层
model.add(tf.keras.layers.Dense(units=1, input_dim=1))
# 查看模型结构
model.summary()

其中 model.summary 函数会输出模型结构，结果如下。

Model: "sequential"
_________________________________________________________________
Layer (type)                 Output Shape              Param #
=================================================================
dense (Dense)                (None, 1)                 2
=================================================================
Total params: 2
Trainable params: 2
Non-trainable params: 0
_________________________________________________________________
100/100 [==============================] - 0s 880us/step - loss: 6.2771

Process finished with exit code 0

接下来，直接使用 .compile 编译模型，指定损失函数为 MSE 平方损失，优化器选择 SGD 随机梯度下降。然后，就可以使用 .fit 传入数据开始迭代了。

model.compile(optimizer='sgd', loss='mse')
model.fit(X, Y, steps_per_epoch=100)

model.fit 输出迭代的结果如下。

100/100 [==============================] - 0s 840us/step - loss: 3.1435

steps_per_epoch 只的是在默认小批量为 32 的条件下，传入相应次数的小批量样本。最终绘制出迭代完成的拟合图像。

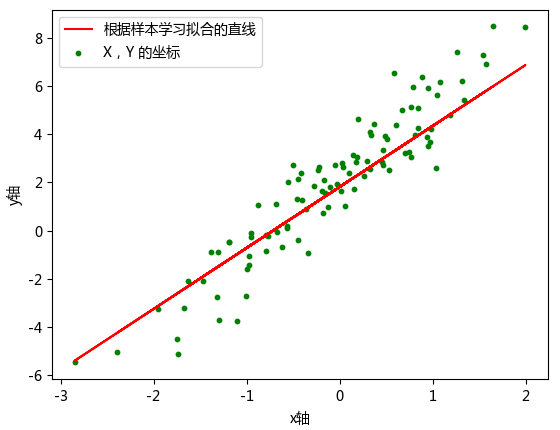
如上所示，完全使用 Keras 高阶 API 实际上只需要 4 行核心代码即可完成。相比于最开始的低阶 API 简化了很多。

使用 Tensorflow 高阶 API keras 实现线性回归的完整代码如下：

import tensorflow as tf
import matplotlib.pyplot as plt
from pylab import mpl

mpl.rcParams['font.sans-serif'] = ['Microsoft YaHei']  # 指定默认字体：解决plot不能显示中文问题
mpl.rcParams['axes.unicode_minus'] = False             # 解决保存图像是负号'-'显示为方块的问题

# 初始化k和b，并生成100个样本
K = 3.0
B = 2.0
NUM_SAMPLES = 100

X = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()      # 初始化随机样本数据X
noise = tf.random.normal(shape=[NUM_SAMPLES, 1]).numpy()  # noise为人为添加的噪声
Y = X * K + B + noise  # 根据X生成随机样本数据Y

# 使用 tf 高阶 API keras
model = tf.keras.Sequential()
# 全连接层
model.add(tf.keras.layers.Dense(units=1, input_dim=1))
# 查看模型结构
model.summary()

model.compile(optimizer='sgd', loss='mse')
model.fit(X, Y, steps_per_epoch=100)

# 画出样本 X 和标签 Y 在坐标上的散点图以及根据样本学习拟合的一条直线
plt.plot(X, model(X), label=u'根据样本学习拟合的直线', c='r')  # 根据样本学习拟合的一条直线
plt.scatter(X, Y, label=u'X，Y 的坐标', color='g', s=10)  # X，Y 的散点坐标
plt.xlabel(u'x轴')
plt.ylabel(u'y轴')
plt.legend()
plt.show()

本节重要知识点

了解线性回归

了解多元非线性回归

了解 TensorFlow 计算线性回归

如果以上内容对您有帮助，请老板用微信扫一下赞赏码，赞赏后加微信号 birdpython 领取免费视频。